olzone.blogg.se

If you are new to Stata we strongly recommend reading all the articles in the Stata Basics section. P′ A – P′ B follows an approximate normal distribution.Ĭalculate the p-value using the normal distribution: p-value = 0.1404.Įstimated proportion for group A: p ′ A = x A n A = 20 200 = 0.1 p ′ A = x A n A = 20 200 = 0.1Įstimated proportion for group B: p ′ B = x B n B = 12 200 = 0.06 p ′ B = x B n B = 12 200 = 0.This article is part of the Stata for Students series. The words is a difference tell you the test is two-tailed.ĭistribution for the test: Since this is a test of two binomial population proportions, the distribution is normal: Random Variable: P′ A – P′ B = difference in the proportions of adult patients who did not react after 30 minutes to Medication A and to Medication B. Then, p A and p B are the desired population proportions. Let A and B be the subscripts for Medication A and Medication B, respectively.

The problem asks for a difference in proportions, making it a test of two proportions. The pooled proportion is calculated as follows: To conduct the test, we use a pooled proportion, p c. Generally, the null hypothesis states that the two proportions are the same.

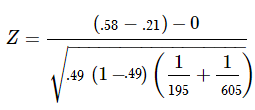
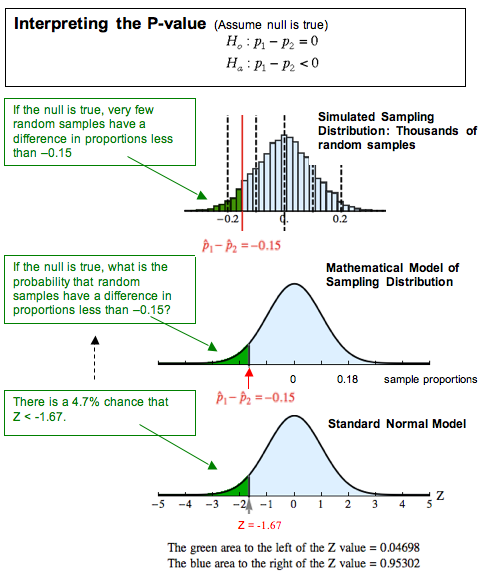
The difference of two proportions follows an approximate normal distribution. A hypothesis test can help determine if a difference in the estimated proportions reflects a difference in the population proportions. If two estimated proportions are different, it may be due to a difference in the populations or it may be due to chance. This keeps each population from being over-sampled and causing incorrect results.Ĭomparing two proportions, like comparing two means, is common.