
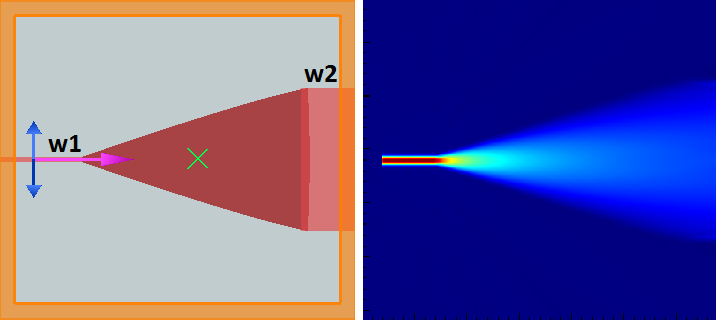
In practice the cell size will often be smaller than this in order to resolve dimensions and features of the structure to be simulated such as the thickness of a substrate or the length of a wire.Īn excitation may be applied to an FDTD simulation in many different ways.
A general rule of thumb sets the minimum resolution, and thus the upper frequency limit, at ten cells per wavelength. The cell size, the dimensions of the small box, is the most important constraint in any FDTD simulation since it determines not only the step size in time, but also the upper frequency limit for the calculation. Each small box shown in the figure represents one FDTD cell. By associating many cell edges with materials, a geometrical structure can be formed within the FDTD grid such as the dielectric sphere shown in Figure 2. Introducing other materials or other configurations is handled in a similar manner and each may be applied to either the electric or magnetic fields depending on the characteristics of the material.
By joining numerous end-to-end cell edges defined as perfectly conducting material, a wire can be formed. For example, to add a perfectly conducting wire segment to a cell edge, the equation for computing the electric field can be replaced by simply setting the field to zero since the electric field in a perfect conductor is identically zero. Within the mesh, materials such as conductors or dielectrics can be added by changing the equations for computing the fields at given locations. Each cell will also have three magnetic fields originating on the faces of the cell adjacent to the common node of the electric fields as shown in Figure 1. The electric fields at the other nine edges of the FDTD cell will belong to other, adjacent cells. Each FDTD cell will overlap edges and faces with its neighbors, so by convention each cell will have three electric fields that begin at a common node associated with it. When many FDTD cells are combined together to form a three-dimensional volume, the result is an FDTD grid or mesh.


 0 kommentar(er)
0 kommentar(er)
